Alireza's blog :: Sit in shade

Sit in shade

Published at: 2024/08/31 13:10:00 - Category: Technology, Web Development

Simple web app to calculate which side of vehicle to sit to minimize sun exposure.

Overview of the Application

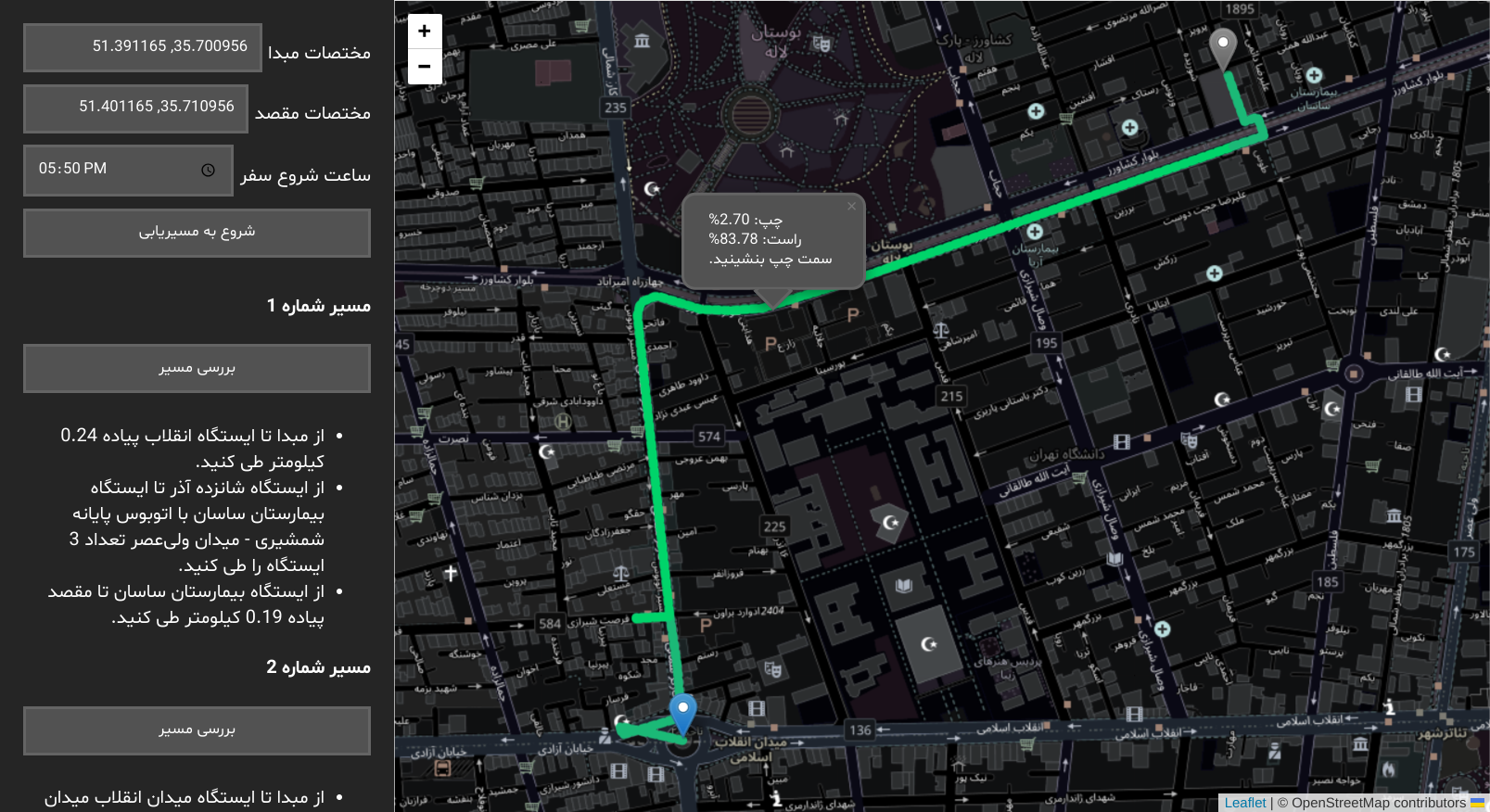
Screenshot of application — Showing bus routes around میدان انقلاب, the app tells the user the perfer the left side to sit.

This web application tries to help users avoid sun exposure during bus travels by calculating which side of a vehicle to sit on based on the sun's position along the route. To achieve this, we combined several technologies: Leaflet.js for the map interface, OpenStreetMap (OSM) for map tiles, SunCalc.js for sun position calculations, and a Python Flask backend to handle route data retrieval.
The app was inspired by SitInShade, which utilizes Google Maps for routing. However, Google Maps' public routing does not function in Iran, prompting the need for a more lcoal solution.

The main components are:

Map Interface: Uses Leaflet.js, utilizing OpenStreetMap (OSM) for map tiles.
Sun Position Calculations: Handled by SunCalc.js, which computes the sun’s azimuth and altitude.
Backend Integration: A Python Flask server fetches and decodes route data from Neshan Maps APIs.
Frontend Logic: JavaScript is used to calculate vectors and determine which side of the vehicle will receive less sunlight.

Step-by-Step Breakdown

1. User Interaction and Map Interface

The user starts by selecting two points: a source and a destination. This map is implemented using Leaflet.js. We used OpenStreetMap (OSM) for the map tiles, providing free and high-quality geographical data (Thank you!).

// Initializing the Leaflet map centered on Tehran
var map = L.map('map').setView([35.6892, 51.3890], 13); // Tehran coordinates
  
L.tileLayer('https://{s}.tile.openstreetmap.org/{z}/{x}/{y}.png', {
    maxZoom: 19,
}).addTo(map);
  
// Adding markers for source and destination
var sourceMarker = L.marker([lat1, lng1]).addTo(map);
var destinationMarker = L.marker([lat2, lng2]).addTo(map);

The user also selects their journey time, which is used in the following caculations.

2. Reverse-Engineering the Neshan Maps API

Here’s where things get interesting. Neshan Maps, a popular mapping service in Tehran, provides the public routing data the app needs. However, their API isn’t publicly documented, so I had to reverse-engineer (a bit of a stretch, not really "Reverse-Engineering", it is easily findable in their webapp.) it to make use of it.

I inspected the API calls made by the Neshan Maps web app using Chrome DevTools. By monitoring the network traffic, I noticed that the API returned cryptic-ish responses for their bus-routing API endpoint in the data section. The data seemed base64, but after decoding did not reveal anything useful.

To crack this, I set up multiple breakpoints in the JavaScript debugger to intercept the request. After the trigger, I stepped through the JS code, arriving at this:

const t = function(e) {
    const t = Int8Array.from(window.atob(e), (e => e.charCodeAt(0)))
      , i = new Int8Array((new TextEncoder).encode("https://rajman.org"))
      , n = t.length
      , o = new Int8Array(n);
    let r = 0;
    for (; r < n; ++r)
        o[r] = t[r] ^ i[r % i.length];
    return JSON.parse((new TextDecoder).decode(o))
}(e);

This piece of JavaScript takes a base64 encoded string (e), decodes it into a byte array, and then performs an XOR operation with a repeating pattern derived from the string "https://rajman.org". The result is then parsed as a JSON object.

Once I understood the decoding process, I wanted to use the API directly and unfortunately I had to deal with CORS, because of this I translated the logic into Python to use Flask as a sort of API proxy:

# Flask route to handle bus routing requests
@app.route('/bus-routing')
def bus_routing():
    headers = {
        'content-type': 'application/json',
        'user-agent': 'Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/126.0.0.0 Safari/537.36',
    }
  
    response = requests.get('https://neshan.org/maps/pwa-api/bus-routing/', params=dict(request.args), headers=headers)
  
    # Decoding response similar to the JavaScript logic found in DevTools
    t = base64.b64decode(response.json()['data'])
    i = list(bytearray("https://rajman.org".encode('utf-8')))
    n = len(t)
    o = [0] * n
  
    for r in range(n):
        o[r] = t[r] ^ i[r % len(i)]
  
    data = bytearray(o).decode('utf-8')
    data = json.loads(data)
  
    return jsonify(data)

In the Python code, we decode the base64 data, then perform the XOR operation exactly as described in the JavaScript code, and finally decode the resulting byte array back into a JSON string.

3. Calculating Sun Position and Vehicle Direction

Once we have the route data, the next step is to calculate the sun's position at various points along the route using SunCalc.js. This library computes the sun's azimuth (horizontal angle) and altitude (vertical angle) based on geographic coordinates (Latitude and longitude) and the specified time.

Here’s a breakdown of how we use this data to determine the optimal side of the vehicle to sit on:

// JavaScript logic to calculate sun exposure along the route
for (let i = 0, j = 1; i < path.length && j < path.length; i++, j++) {
    lat1 = radians(path[i]['lat']);
    lng1 = radians(path[i]['lng']);
    lat2 = radians(path[j]['lat']);
    lng2 = radians(path[j]['lng']);
  
    const sunPos = SunCalc.getPosition(datetime, path[i]['lat'], path[i]['lng']);
    azimuth = sunPos['azimuth'];
    altitude = sunPos['altitude'];
  
    // If the sun is below the horizon, skip this calculation
    if (altitude < 0) continue;
  
    // Calculate the direction vector of the vehicle
    dlng = lng2 - lng1;
    x = Math.cos(lat2) * Math.sin(dlng);
    y = Math.cos(lat1) * Math.sin(lat2) - Math.sin(lat1) * Math.cos(lat2) * Math.cos(dlng);
    z = 0;
  
    magnitude = Math.sqrt(x ** 2 + y ** 2);
    const vehicle_vector = [x / magnitude, y / magnitude, z];
  
    // Calculate the direction vector of the sun
    x = Math.cos(altitude) * Math.sin(azimuth);
    y = Math.cos(altitude) * Math.cos(azimuth);
    z = Math.sin(altitude);
  
    magnitude = Math.sqrt(x ** 2 + y ** 2 + z ** 2);
    const sun_vector = [x / magnitude, y / magnitude, z / magnitude];
  
    // Determine if the sun is on the left or right side of the vehicle
    const cross_product = vehicle_vector[0] * sun_vector[1] - vehicle_vector[1] * sun_vector[0];
    if (cross_product > 0) {
        left += 1;
    } else if (cross_product < 0) {
        right += 1;
    }
}

The application determines which side of the vehicle will be in the shade by calculating the relative positions of the sun and the vehicle along the selected route. This involves several mathematical computations, primarily using vectors and trigonometry.

3. 1. Vehicle Direction Calculation

First, we calculate the direction of the vehicle between two consecutive points on the route. Let's denote two consecutive points on the path as $ P_1 = (\text{lat}_1, \text{lng}_1) $ and $ P_2 = (\text{lat}_2, \text{lng}_2) $. To compute the direction of the vehicle, we convert these geographic coordinates (latitude and longitude) to radians:

$$ \text{lat}_1 = \text{radians}(\text{lat}_1), \quad \text{lng}_1 = \text{radians}(\text{lng}_1) $$

$$ \text{lat}_2 = \text{radians}(\text{lat}_2), \quad \text{lng}_2 = \text{radians}(\text{lng}_2) $$

Next, we calculate the difference in longitude:

$$ \Delta \text{lng} = \text{lng}_2 - \text{lng}_1 $$

Using the Haversine formula components, we compute the direction vector of the vehicle:

$$ x = \cos(\text{lat}_2) \cdot \sin(\Delta \text{lng}) $$ $$ y = \cos(\text{lat}_1) \cdot \sin(\text{lat}_2) - \sin(\text{lat}_1) \cdot \cos(\text{lat}_2) \cdot \cos(\Delta \text{lng}) $$

The vehicle's directional vector $ \mathbf{V} $ is then normalized:

$$ \mathbf{V} = \left( \frac{x}{\sqrt{x^2 + y^2}}, \frac{y}{\sqrt{x^2 + y^2}}, 0 \right) $$

3. 2. Sun Position Calculation

We use the SunCalc library to determine the sun's position at a specific date and time at the location $ P_1 $. The SunCalc provides the sun's azimuth ($ \theta $) and altitude ($ \alpha $) angles. The sun's position vector $ \mathbf{S} $ in 3D Cartesian coordinates is calculated as:

$$ x = \cos(\alpha) \cdot \sin(\theta) $$ $$ y = \cos(\alpha) \cdot \cos(\theta) $$ $$ z = \sin(\alpha) $$

The sun's directional vector $ \mathbf{S} $ is then normalized:

$$ \mathbf{S} = \left( \frac{x}{\sqrt{x^2 + y^2 + z^2}}, \frac{y}{\sqrt{x^2 + y^2 + z^2}}, \frac{z}{\sqrt{x^2 + y^2 + z^2}} \right) $$

3. 3. Determining the Shaded Side

To determine which side of the vehicle (left or right) will be shaded, we compute the cross product of the vehicle's directional vector $ \mathbf{V} $ and the sun's directional vector $ \mathbf{S} $:

$$ \mathbf{V} \times \mathbf{S} = \left( \mathbf{V}_y \cdot \mathbf{S}_z - \mathbf{V}_z \cdot \mathbf{S}_y, \mathbf{V}_z \cdot \mathbf{S}_x - \mathbf{V}_x \cdot \mathbf{S}_z, \mathbf{V}_x \cdot \mathbf{S}_y - \mathbf{V}_y \cdot \mathbf{S}_x \right) $$

Since both vectors lie in the horizontal plane (where $ z = 0 $ for the vehicle vector), the cross product simplifies to:

$$ \mathbf{V} \times \mathbf{S} = \mathbf{V}_x \cdot \mathbf{S}_y - \mathbf{V}_y \cdot \mathbf{S}_x $$

The sign of the cross product's $ z $-component determines the relative direction of the sun to the vehicle's movement:

If the cross product is positive, the sun is on the right side of the vehicle.
If the cross product is negative, the sun is on the left side of the vehicle.

By aggregating these results along the route, the application suggests which side of the vehicle (left or right) will generally be less exposed to the sun, allowing to choose the more shaded side.
If the value falls within a certain threshold, it is considered equal, meaning neither side is preferred.

4. Rendering Results

After processing the entire route, the application aggregates the results and determines which side of the vehicle has the least sun exposure. This information is then presented to the user via popups on centers of each bus route.

Limitations and Future Enhancements

While the application provides useful guidance, it currently doesn’t account for foctors like real-time traffic, varying speeds, or route changes that could change the duration of route and the side of the sun. The sun's position is calculated based on fixed intervals along the route without considering these variables.